ocp_flatten.hpp File Reference

Reformulate an optimal control problem on a Lie group as an optimal control problem in the tangent space around a reference trajectory. More...

#include <Eigen/Core>
#include <Eigen/Sparse>
#include <smooth/bundle.hpp>
#include <smooth/diff.hpp>
#include "ocp.hpp"
#include "smooth/lie_sparse.hpp"
#include "utils/sparse.hpp"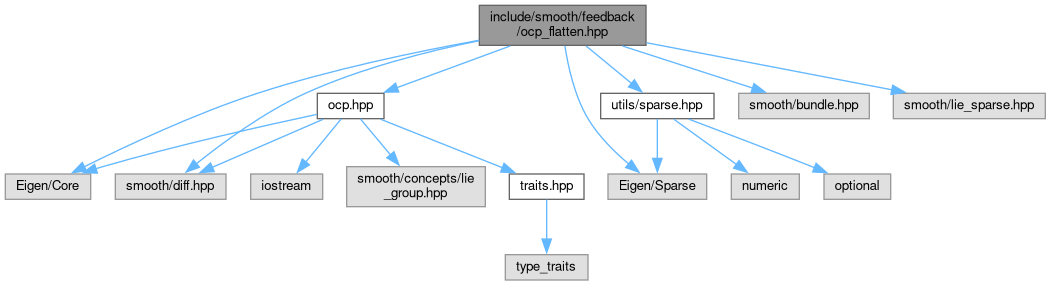

Include dependency graph for ocp_flatten.hpp:

Go to the source code of this file.

Functions
auto	smooth::feedback::flatten_ocp (const OCPType auto &ocp, auto &&xl, auto &&ul)
	Flatten a LieGroup OCP by defining it in the tangent space around a trajectory. More...
template<LieGroup X, Manifold U>
auto	smooth::feedback::unflatten_ocpsol (const auto &flatsol, auto &&xl_fun, auto &&ul_fun)
	Unflatten a FlatOCPSolution. More...

Detailed Description

Reformulate an optimal control problem on a Lie group as an optimal control problem in the tangent space around a reference trajectory.

Todo:

More efficient implementation of Hessian in FlatDyn.

Accept dxl as a template argument to avoid double differentiation.

Definition in file ocp_flatten.hpp.

Function Documentation

flatten_ocp()

auto smooth::feedback::flatten_ocp	(	const OCPType auto &	ocp,
		auto &&	xl,
		auto &&	ul
	)

Flatten a LieGroup OCP by defining it in the tangent space around a trajectory.

Parameters

ocp	OCPType defined on a LieGroup
xl	nominal state trajectory
ul	nominal state trajectory

Note

The flattened problem defines analytical jacobians and hessians if ocp does.

@warn The Hessian of the flattened dynamics is not implemented in an efficient manner.

Returns

FlatOCPType in variables (xe, ue) obtained via variables change x = xl ⊕ xe, u = ul ⊕ ue,

Definition at line 513 of file ocp_flatten.hpp.

unflatten_ocpsol()

template<LieGroup X, Manifold U>

auto smooth::feedback::unflatten_ocpsol	(	const auto &	flatsol,
		auto &&	xl_fun,
		auto &&	ul_fun
	)

Unflatten a FlatOCPSolution.

If flat_sol is a solution to flat_ocp = flatten_ocp(ocp, xl_fun, ul_fun), then unflatten_ocpsol(flat_sol, xl_fun, ul_fun) is a solution to ocp.

Definition at line 550 of file ocp_flatten.hpp.