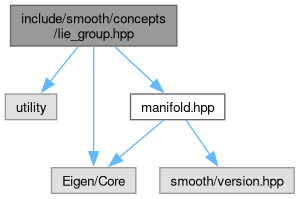
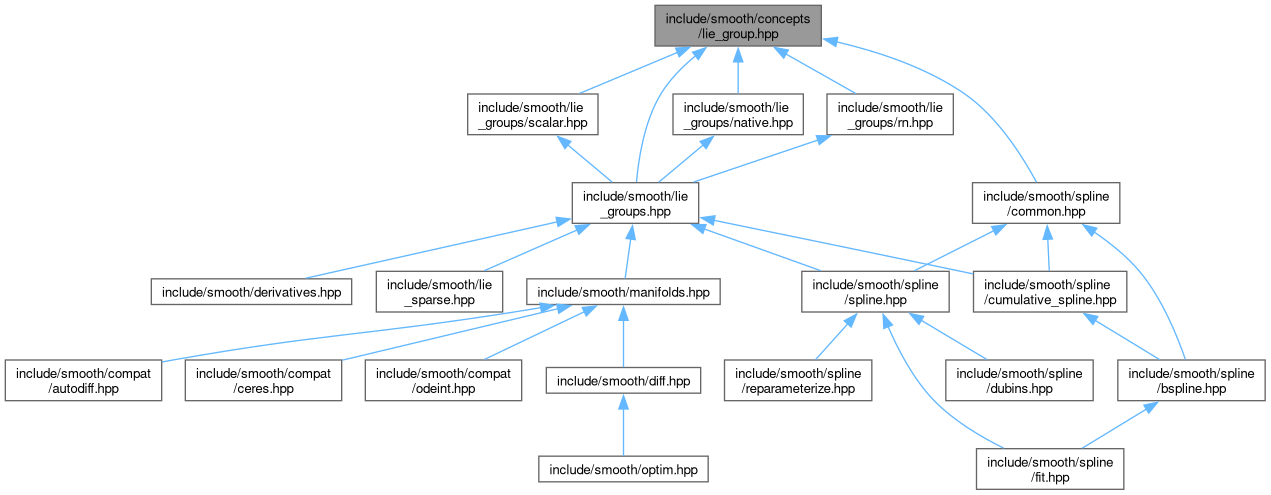
Go to the source code of this file.
Classes | |
| struct | traits::man< G > |
| Manifold interface for LieGroup types (all LieGroups are also Manifolds). More... | |
Concepts | |
| concept | LieGroup |
| Class-external Lie group interface defined through the traits::lie trait class. | |
Functions | |
| template<LieGroup G> | |
| PlainObject< G > | Identity (Eigen::Index dof) |
| Identity in Lie group. | |
| template<LieGroup G> requires (Dof<G> > 0) | |
| PlainObject< G > | Identity () |
| Identity in Lie group with static Dof. | |
| template<LieGroup G> | |
| PlainObject< G > | Random (Eigen::Index dof) |
| Random element in Lie group. | |
| template<LieGroup G> requires (Dof<G> > 0) | |
| PlainObject< G > | Random () |
| Random element in Lie group with static Dof. | |
| template<LieGroup G> | |
| TangentMap< G > | Ad (const G &g) |
| Group adjoint \( Ad_g a \coloneq (G * \hat(a) * G^{-1})^{\wedge} \). | |
| template<LieGroup G, typename Arg > | |
| PlainObject< G > | composition (const G &g, Arg &&a) |
| Group binary composition. | |
| template<LieGroup G, typename Arg , typename... Args> | |
| PlainObject< G > | composition (const G &g, Arg &&a, Args &&... as) |
| Group multinary composition. | |
| template<LieGroup G> | |
| PlainObject< G > | inverse (const G &g) |
| Group inverse. | |
| template<LieGroup G, typename Arg > | |
| bool | isApprox (const G &g, Arg &&a, typename traits::lie< G >::Scalar eps=Eigen::NumTraits< typename traits::lie< G >::Scalar >::dummy_precision()) |
| Check if two group elements are approximately equal. | |
| template<LieGroup G> | |
| Tangent< G > | log (const G &g) |
| Group logarithm. | |
| template<LieGroup G, typename Arg > | |
| TangentMap< G > | ad (Arg &&a) |
| Lie algebra adjoint \( ad_a b = [a, b] \). | |
| template<LieGroup G, typename Arg > | |
| PlainObject< G > | exp (Arg &&a) |
| Lie algebra exponential. | |
| template<LieGroup G, typename Arg > | |
| TangentMap< G > | dr_exp (Arg &&a) |
| Right Jacobian of exponential map. | |
| template<LieGroup G, typename Arg > | |
| TangentMap< G > | dr_expinv (Arg &&a) |
| Right Jacobian of exponential map inverse. | |
| template<LieGroup G, typename Arg > | |
| Hessian< G > | d2r_exp (Arg &&a) |
| Right Hessian of exponential map. | |
| template<LieGroup G, typename Arg > | |
| Hessian< G > | d2r_expinv (Arg &&a) |
| Right Hessian of exponential map inverse. | |
| template<LieGroup G, typename Derived > | |
| PlainObject< G > | lplus (const G &g, const Eigen::MatrixBase< Derived > &a) |
| Left-plus. | |
| template<LieGroup G, LieGroup Go> | |
| Tangent< G > | lminus (const G &g1, const Go &g2) |
| Left-minus. | |
| template<LieGroup G, typename Derived > | |
| TangentMap< G > | dl_exp (const Eigen::MatrixBase< Derived > &a) |
| Left Jacobian of exponential map. | |
| template<LieGroup G, typename Derived > | |
| TangentMap< G > | dl_expinv (const Eigen::MatrixBase< Derived > &a) |
| Left Jacobian of exponential map inverse. | |
| template<LieGroup G, typename Derived > | |
| Hessian< G > | d2l_exp (const Eigen::MatrixBase< Derived > &a) |
| Left Hessian of exponential map. | |
| template<LieGroup G, typename Derived > | |
| Hessian< G > | d2l_expinv (const Eigen::MatrixBase< Derived > &a) |
| Left Hessian of exponential map inverse. | |
Detailed Description
Internal and external LieGroup interfaces and free LieGroup functions.
Definition in file lie_group.hpp.
Function Documentation
◆ ad()
|
inline |
Lie algebra adjoint \( ad_a b = [a, b] \).
Definition at line 247 of file lie_group.hpp.
◆ Ad()
|
inline |
Group adjoint \( Ad_g a \coloneq (G * \hat(a) * G^{-1})^{\wedge} \).
Definition at line 186 of file lie_group.hpp.
◆ composition() [1/2]
|
inline |
Group binary composition.
Definition at line 195 of file lie_group.hpp.
◆ composition() [2/2]
|
inline |
Group multinary composition.
Definition at line 204 of file lie_group.hpp.
◆ d2l_exp()
|
inline |
Left Hessian of exponential map.
Definition at line 341 of file lie_group.hpp.
◆ d2l_expinv()
|
inline |
Left Hessian of exponential map inverse.
Definition at line 350 of file lie_group.hpp.
◆ d2r_exp()
Right Hessian of exponential map.
Definition at line 285 of file lie_group.hpp.
◆ d2r_expinv()
Right Hessian of exponential map inverse.
Definition at line 294 of file lie_group.hpp.
◆ dl_exp()
|
inline |
Left Jacobian of exponential map.
Definition at line 323 of file lie_group.hpp.
◆ dl_expinv()
|
inline |
Left Jacobian of exponential map inverse.
Definition at line 332 of file lie_group.hpp.
◆ dr_exp()
|
inline |
Right Jacobian of exponential map.
Definition at line 267 of file lie_group.hpp.
◆ dr_expinv()
|
inline |
Right Jacobian of exponential map inverse.
Definition at line 276 of file lie_group.hpp.
◆ exp()
|
inline |
◆ Identity() [1/2]
requires (Dof<G> > 0)
|
inline |
Identity in Lie group with static Dof.
Definition at line 162 of file lie_group.hpp.
◆ Identity() [2/2]
|
inline |
Identity in Lie group.
- Parameters
-
dof degrees of freedom
Definition at line 152 of file lie_group.hpp.
◆ inverse()
|
inline |
Group inverse.
Definition at line 213 of file lie_group.hpp.
◆ isApprox()
|
inline |
Check if two group elements are approximately equal.
Definition at line 222 of file lie_group.hpp.
◆ lminus()
Left-minus.
Definition at line 314 of file lie_group.hpp.
◆ log()
◆ lplus()
|
inline |
Left-plus.
Definition at line 305 of file lie_group.hpp.
◆ Random() [1/2]
requires (Dof<G> > 0)
|
inline |
Random element in Lie group with static Dof.
Definition at line 180 of file lie_group.hpp.
◆ Random() [2/2]
|
inline |
Random element in Lie group.
- Parameters
-
dof degrees of freedom
Definition at line 170 of file lie_group.hpp.