derivatives.hpp File Reference

Various useful derivatives. More...

#include <Eigen/Core>
#include "lie_groups.hpp"
#include "detail/derivatives_impl.hpp"

Include dependency graph for derivatives.hpp:

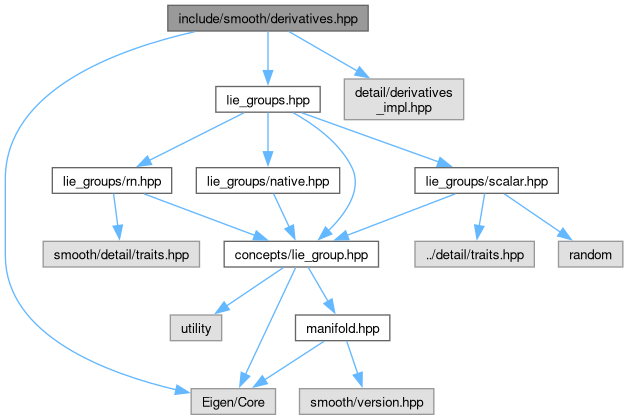
Go to the source code of this file.

Functions
template<typename At , typename dAt , typename Bt , typename dBt >
SMOOTH_BEGIN_NAMESPACE auto	d_matrix_product (const At &A, const dAt &dA, const Bt &B, const dBt &dB)
	Derivative of matrix product.
template<typename JfT , typename HfT , typename JgT , typename HgT >
auto	d2_fog (const JfT &Jf, const HfT &Hf, const JgT &Jg, const HgT &Hg)
	Hessian of composed function \( (f \circ g)(x) \).
template<LieGroup G>
TangentMap< G >	dr_rminus (const Tangent< G > &e)
	Jacobian of rminus.
template<LieGroup G>
Hessian< G >	d2r_rminus (const Tangent< G > &e)
	Hessian of rminus.
template<LieGroup G>
Eigen::RowVector< Scalar< G >, Dof< G > >	dr_rminus_squarednorm (const Tangent< G > &e)
	Jacobian of the squared norm of rminus.
template<LieGroup G>
Eigen::Matrix< Scalar< G >, Dof< G >, Dof< G > >	d2r_rminus_squarednorm (const Tangent< G > &e)
	Hessian of the squared norm of rminus.

Detailed Description

Various useful derivatives.

Definition in file derivatives.hpp.

Function Documentation

d2_fog()

template<typename JfT , typename HfT , typename JgT , typename HgT >

auto d2_fog	(	const JfT &	Jf,
		const HfT &	Hf,
		const JgT &	Jg,
		const HgT &	Hg
	)

Hessian of composed function \( (f \circ g)(x) \).

Parameters

Jf	Jacobian of f at y = g(x) [No x Ny ]
Hf	Hessian of f at y = g(x) [Ny x No*Ny]
Jg	Jacobian of g at x [Ny x Nx ]
Hg	Hessian of g at x [Nx x Ny*Nx]

Returns

Hessian of size [No x No*Nx]

d2r_rminus()

template<LieGroup G>

Hessian< G > d2r_rminus

(

const Tangent< G > &

e

)

Hessian of rminus.

Parameters

e	value of \( x \ominus_r y \)

Returns

\( \mathrm{d}^{2r} (x \ominus_r y)_{xx} \)

d2r_rminus_squarednorm()

template<LieGroup G>

Eigen::Matrix< Scalar< G >, Dof< G >, Dof< G > > d2r_rminus_squarednorm

(

const Tangent< G > &

e

)

Hessian of the squared norm of rminus.

Parameters

e	value of \( x \ominus_r y \)

Returns

\( \mathrm{d}^{2r} \left( \frac{1}{2} \| x \ominus_r y \|^2 \right)_{xx} \)

d_matrix_product()

template<typename At , typename dAt , typename Bt , typename dBt >

SMOOTH_BEGIN_NAMESPACE auto d_matrix_product	(	const At &	A,
		const dAt &	dA,
		const Bt &	B,
		const dBt &	dB
	)

Derivative of matrix product.

Parameters

A	matrix [N x K]
dA	derivative of A on horizontal Hessian form [K x N*Nvar]
B	matrix [K x M]
dB	derivative of B on horizontal Hessian form [M x K*Nvar]

Returns

derivative of A * B on horizontal Hessian form

dr_rminus()

template<LieGroup G>

TangentMap< G > dr_rminus

(

const Tangent< G > &

e

)

Jacobian of rminus.

Parameters

e	value of \( x \ominus_r y \)

Returns

\( \mathrm{d}^{r} (x \ominus_r y)_{x} \)

dr_rminus_squarednorm()

template<LieGroup G>

Eigen::RowVector< Scalar< G >, Dof< G > > dr_rminus_squarednorm

(

const Tangent< G > &

e

)

Jacobian of the squared norm of rminus.

Parameters

e	value of \( x \ominus_r y \)

Returns

\( \mathrm{d}^r \left( \frac{1}{2} \| x \ominus_r y \|^2 \right)_x \)