diff.hpp File Reference

Differentiation on Manifolds. More...

#include <utility>
#include "manifolds.hpp"
#include "wrt.hpp"
#include "detail/diff_impl.hpp"

Include dependency graph for diff.hpp:

This graph shows which files directly or indirectly include this file:

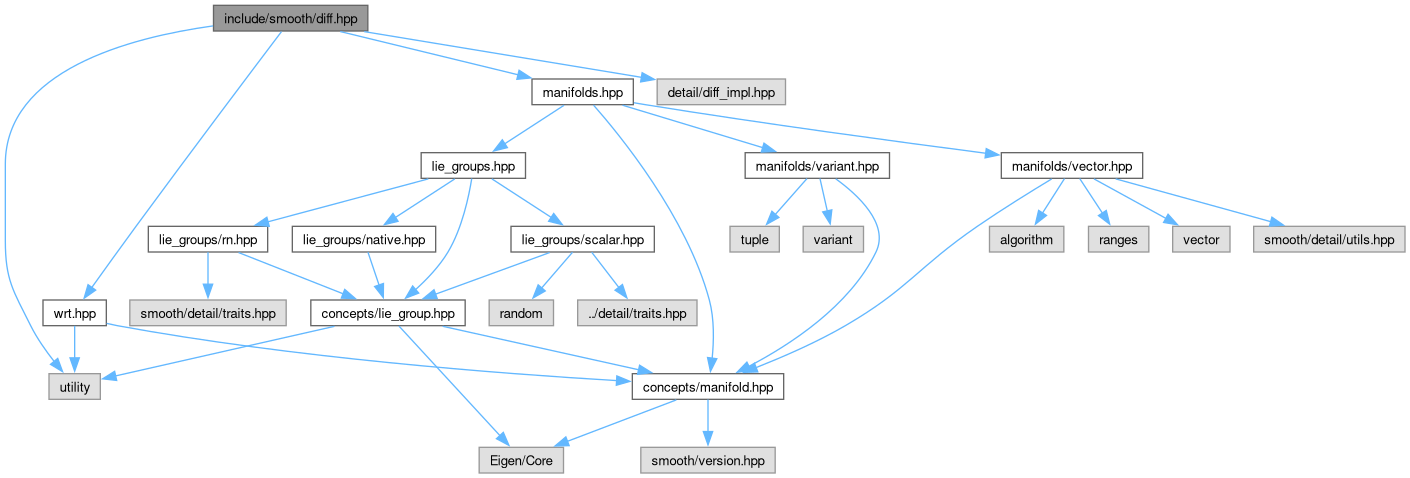
Go to the source code of this file.

Enumerations
enum class	diff::Type { Numerical , Autodiff , Ceres , Analytic , Default }
	Available differentiation methods. More...

Functions
template<std::size_t K, Type D>
auto	diff::dr (auto &&f, auto &&x)
	Differentiation in tangent space.
template<std::size_t K, Type D, std::size_t... Idx>
auto	diff::dr (auto &&f, auto &&x, std::index_sequence< Idx... > idx)
	Differentiation in tangent space.
template<std::size_t K>
auto	diff::dr (auto &&f, auto &&x)
	Differentiation in tangent space using default method.
template<std::size_t K, std::size_t... Idx>
auto	diff::dr (auto &&f, auto &&x, std::index_sequence< Idx... > idx)
	Differentiation in tangent space using default method.

Detailed Description

Differentiation on Manifolds.

Definition in file diff.hpp.

Enumeration Type Documentation

Type

enum class diff::Type

strong

Available differentiation methods.

Enumerator
Numerical	Numerical (forward) derivatives.
Autodiff	Uses the autodiff (https://autodiff.github.io) library; requires compat/autodiff.hpp
Ceres	Uses the Ceres (http://ceres-solver.org) built-in autodiff; requires compat/ceres.hpp
Analytic	Hand-coded derivative. Type must have a function named 'jacobian' : x -> Mat (order 1) and 'hesssian': x -> Mat (order 2) that compute the derivatives.
Default	Select based on availability (Analytic > Autodiff > Ceres > Numerical)

Definition at line 21 of file diff.hpp.

Function Documentation

dr() [1/4]

template<std::size_t K, Type D>

auto diff::dr	(	auto &&	f,
		auto &&	x
	)

Differentiation in tangent space.

Template Parameters

K	differentiation order (0, 1 or 2)
D	differentiation method to use

First derivatives are returned as a matrix df s.t. df(i, j) = dfi / dxj, where fi is the i:th degree of freedom of f, and xj the j:th degree of freedom of x.

Second derivatives are stored as a horizontally stacked block matrix d2f = [ d2f0 d2f1 ... d2fN ], where d2fi(j, k) = d2fi / dxjxk is the Hessian of the i:th degree of freedom of f.

Parameters

f	function to differentiate
x	reference tuple of function arguments

Returns

{f(x)} for K = 0, {f(x), dr f(x)} for K = 1, {f(x), dr f(x), d2r f(x)} for K = 2

Note

Only scalar functions suppored for K = 2

All arguments in x as well as the return type \(f(x)\) must satisfy the Manifold concept.

dr() [2/4]

template<std::size_t K>

auto diff::dr	(	auto &&	f,
		auto &&	x
	)

Differentiation in tangent space using default method.

Template Parameters

K	differentiation order

Parameters

f	function to differentiate
x	reference tuple of function arguments

Returns

std::pair containing value and right derivative: \((f(x), \mathrm{d}^r f_x)\)

Note

All arguments in x as well as the return type \(f(x)\) must satisfy the Manifold concept.

dr() [3/4]

template<std::size_t K, Type D, std::size_t... Idx>

auto diff::dr	(	auto &&	f,
		auto &&	x,
		std::index_sequence< Idx... >	idx
	)

Differentiation in tangent space.

Like above, but calculate a subset idx of derivatives.

Parameters

f	function to differentiate
x	reference tuple of function arguments
idx	indices defining subset of x

dr() [4/4]

template<std::size_t K, std::size_t... Idx>

auto diff::dr	(	auto &&	f,
		auto &&	x,
		std::index_sequence< Idx... >	idx
	)

Differentiation in tangent space using default method.

Like above, but calculate a subset idx of derivatives.

Parameters

f	function to differentiate
x	reference tuple of function arguments
idx	indices defining subset of x