fit.hpp File Reference

Fit Spline and Bspline from data. More...

#include <ranges>
#include "bspline.hpp"
#include "spline.hpp"
#include "detail/fit_impl.hpp"

Include dependency graph for fit.hpp:

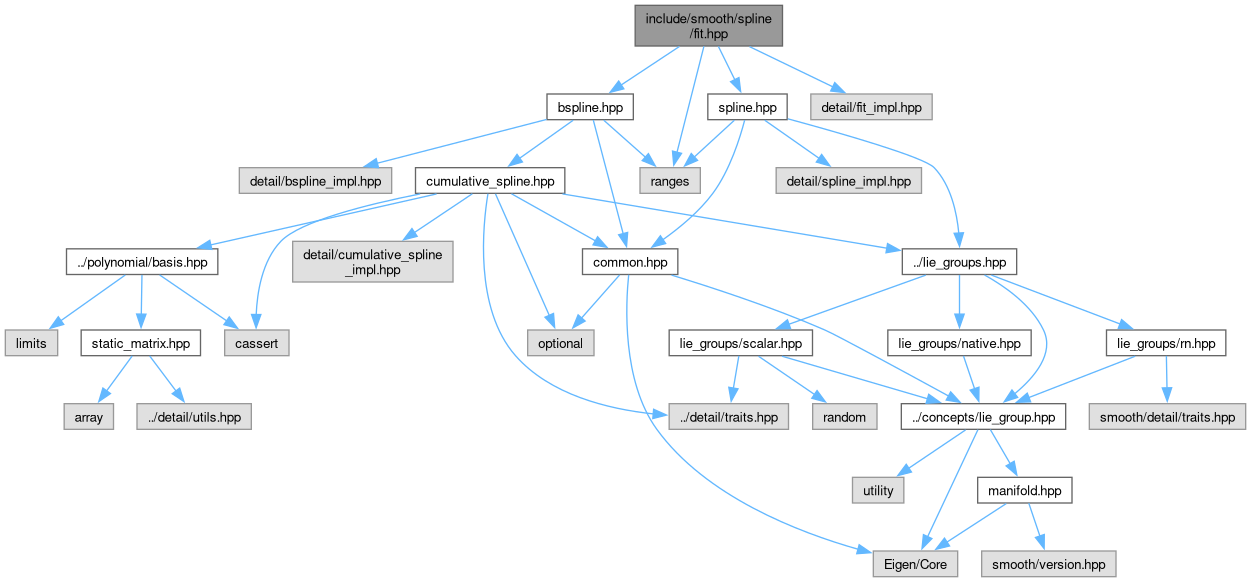
Go to the source code of this file.

Classes
struct	spline_specs::NoConstraints< G, K >
	SplineSpec without boundary constraints. More...
struct	spline_specs::FixedDerCubic< G, P1, P2 >
	SplineSpec for a cubic spline with two boundary conditions. More...
struct	spline_specs::MinDerivative< G, K, O, P >
	SplineSpec for optimized spline. More...

Concepts
concept	SplineSpec
	Spline specification.

Typedefs
template<LieGroup G>
using	spline_specs::PiecewiseConstant = NoConstraints< G, 0 >
	SplineSpec for a piecewise constant function.
template<LieGroup G>
using	spline_specs::PiecewiseLinear = NoConstraints< G, 1 >
	SplineSpec for a piecewise linear function.

Functions
Eigen::VectorXd	fit_spline_1d (std::ranges::sized_range auto &&dt_r, std::ranges::sized_range auto &&dx_r, const SplineSpec auto &ss)
	Find N degree K Bernstein polynomials p_i(t) for i = 0, ..., N s.t that satisfies constraints and s.t.
auto	fit_spline (std::ranges::random_access_range auto &&ts, std::ranges::random_access_range auto &&gs, const SplineSpec auto &ss)
	Fit a Spline to given points.
auto	fit_spline_cubic (std::ranges::range auto &&ts, std::ranges::range auto &&gs)
	Fit a cubic Spline with natural boundary conditions.
template<int K>
auto	fit_bspline (std::ranges::range auto &&ts, std::ranges::range auto &&gs, const double dt)
	Fit a bpsline to data points \((t_i, g_i)\) by solving the optimization problem.

Detailed Description

Fit Spline and Bspline from data.

Definition in file fit.hpp.

Typedef Documentation

PiecewiseConstant

template<LieGroup G>

using spline_specs::PiecewiseConstant = typedef NoConstraints<G, 0>

SplineSpec for a piecewise constant function.

Definition at line 61 of file fit.hpp.

PiecewiseLinear

template<LieGroup G>

using spline_specs::PiecewiseLinear = typedef NoConstraints<G, 1>

SplineSpec for a piecewise linear function.

Definition at line 65 of file fit.hpp.

Function Documentation

fit_bspline()

template<int K>

auto fit_bspline	(	std::ranges::range auto &&	ts,
		std::ranges::range auto &&	gs,
		const double	dt
	)

Fit a bpsline to data points \((t_i, g_i)\) by solving the optimization problem.

\[ \min_{p} \left\| p(t_i) - g_i \right\|^2 \]

Template Parameters

K	bspline degree

Parameters

ts	time values t_i (doubles, strictly increasing)
gs	data values t_i
dt	distance between spline control points

Returns

BSpline of order K that approximates data

Note

Allocates heap memory.

fit_spline()

auto fit_spline	(	std::ranges::random_access_range auto &&	ts,
		std::ranges::random_access_range auto &&	gs,
		const SplineSpec auto &	ss
	)

Fit a Spline to given points.

Template Parameters

G	LieGroup
K	Spline degree

Parameters

ts	range of times
gs	range of values
ss	spline specification

Returns

Spline c s.t. \( c(t_i) = g_i \) for \((t_i, g_i) \in zip(ts, gs) \)

Note

Allocates heap memory.

fit_spline_1d()

Eigen::VectorXd fit_spline_1d	(	std::ranges::sized_range auto &&	dt_r,
		std::ranges::sized_range auto &&	dx_r,
		const SplineSpec auto &	ss
	)

Find N degree K Bernstein polynomials p_i(t) for i = 0, ..., N s.t that satisfies constraints and s.t.

\[ p_i(0) = 0 \\ p_i(\delta t) = \delta x \]

Parameters

dt_r	range of parameter differences \( \delta_t \)
dx_r	range of value differences \( \delta_x \)
ss	spline specification

Returns

vector \( \alpha \) of size (K + 1) * N s.t. \( \beta = \alpha_{i (K + 1): (i + 1) (K + 1) } \) defines polynomial \( p_i \) as

\[ p_i(t) = \sum_{\nu = 0}^K \beta_\nu b_{\nu, k} \left( \frac{t}{\delta t} \right), \]

where \( \delta t \) is the i:th member of dt_r.

Note

Allocates heap memory.

fit_spline_cubic()

auto fit_spline_cubic	(	std::ranges::range auto &&	ts,
		std::ranges::range auto &&	gs
	)

Fit a cubic Spline with natural boundary conditions.

Parameters

ts	range of times
gs	range of values

Returns

Spline c s.t. \( c(t_i) = g_i \) for \((t_i, g_i) \in zip(ts, gs) \)

Cubic spline that approximates data

Note

Allocates heap memory.