Lie Theory for Robotics

• Requirements: C++20, Eigen 3.4
• Documentation
• Compatible with: autodiff, boost::numeric::odeint, Ceres, ROS
• Written in an extensible functional programming style

In robotics it is often convenient to work in non-Euclidean manifolds. Lie groups are a class of manifolds that are easy to work with due to their symmetries, and that are also good models for many robotic systems. This header-only C++20 library facilitates leveraging Lie theory in robotics software, by enabling:

• Algebraic manipulation
• Automatic differentiation
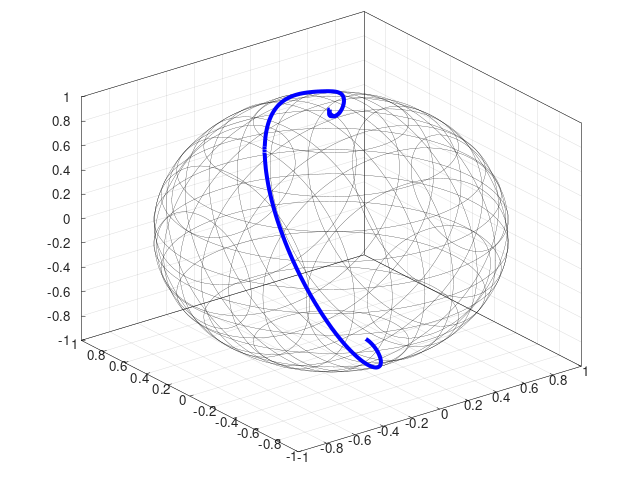
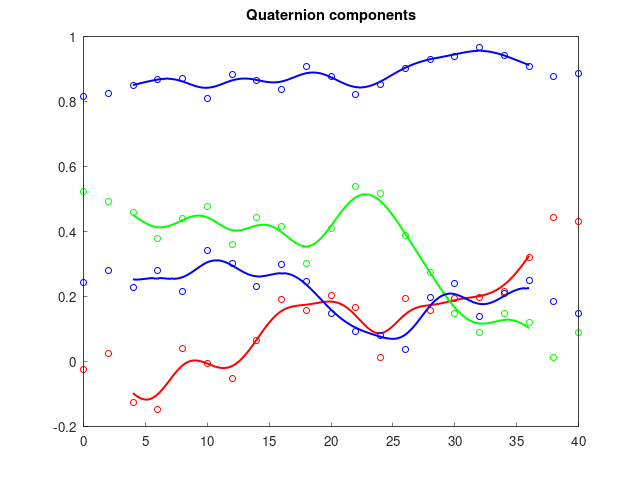
• Interpolation (right figure shows a B-spline of order 5 on smooth::SO3, see examples/bspline.cpp)
• Numerical integration (left figure shows the solution of an ODE on , see examples/odeint.cpp)
• Optimization

The following common Lie groups are implemented:

• smooth::SO2: two-dimensional rotations with complex number memory representation
• smooth::SO3: three-dimensional rotations with quaternion memory representation
• smooth::SE2: two-dimensional rigid motions
• smooth::SE3: three-dimensional rigid motions
• smooth::C1: complex numbers (excluding zero) under multiplication
• smooth::Galilei: the Galilean group. It includes SE_2(3) as a special case.
• smooth::SE_K_3: generalization of SE3 with multiple translations
• A smooth::Bundle type to treat Lie group products as a single Lie group. The Bundle type also supports regular Eigen vectors as components
• Lie group interfaces for Eigen vectors and builtin scalars

Getting started

Download and Build

Clone the repository and install it

git clone https://github.com/pettni/smooth.git
cd smooth
mkdir build && cd build
 
# Specify a C++20-compatible compiler if your default does not support C++20.
# Build tests and/or examples as desired.
cmake .. -DBUILD_EXAMPLES=OFF -DBUILD_TESTS=OFF
make -j8
sudo make install

Alternatively, if using ROS or ROS2 just clone smooth into a catkin/colcon workspace source folder and build the workspace with a compiler that supports C++20. Example with colcon:

colcon build --cmake-args -DCMAKE_CXX_COMPILER=/usr/bin/g++-10

Use with cmake

To utilize smooth in your own project, include something along these lines in your CMakeLists.txt

find_package(smooth)
 
add_executable(my_executable main.cpp)
target_link_libraries(my_executable smooth::smooth)

Explore the API

Check out the Documentation and the examples.

Using the library

Algebraic Manipulations

// Also works with other types: SO2d, SE2d, SE3d, Bundle<SO3d, T3d> etc...
 
using Tangent = typename smooth::SO3d::Tangent;
 
// construct a random group element and a random tangent element
smooth::SO3d g = smooth::SO3d::Random();
Tangent a = Tangent::Random();
 
// lie group exponential
auto exp_a = smooth::SO3d::exp(a);
 
// lie group logarithm
auto g_log = g.log();
 
// lie algebra hat and vee maps
auto a_hat = smooth::SO3d::hat(a);
auto a_hat_vee = smooth::SO3d::vee(a_hat);
 
// group adjoint
auto Ad_g = g.Ad();
 
// lie algebra adjoint
auto ad_a = smooth::SO3d::ad(a);
 
// derivatives of the exponential map
auto dr_exp_v = smooth::SO3d::dr_exp(a);   // right derivative
auto dl_exp_v = smooth::SO3d::dl_exp(a);   // left derivative
auto dr_expinv_v = smooth::SO3d::dr_expinv(a);   // inverse of right derivative
auto dl_expinv_v = smooth::SO3d::dl_expinv(a);   // inverse of left derivative
 
// group action
Eigen::Vector3d v = Eigen::Vector3d::Random();
auto v_transformed = g * v;
 
// memory mapping using Eigen::Map
std::array<double, smooth::SO3d::RepSize> mem;
Eigen::Map<const smooth::SO3d> m_g(mem.data());

Concepts and Types

These C++20 concepts are implemented in concepts.hpp.

• Manifold: type for which rplus (geodesic addition) and rminus (geodesic subtraction) are defined. Examples:
  • All LieGroup types
  • std::vector<Manifold> is a Manifold defined in manifold_vector.hpp—it facilitates e.g. optimization and differentiation w.r.t. a dynamic number of Manifolds
  • std::variant<Manifold ...> is a Manifold defined in manifold_variant.hpp. Using std::vector<std::variant<Manifold...>> can be convenient when optimizing over variables with different parameterizations.
• LieGroup: type for which Lie group operations (exp, log, Ad, etc...) are defined. Examples:
  • All NativeLieGroup types
  • Fixed-size Eigen vectors (e.g. Eigen::Vector3d)
  • Dynamic-size Eigen vectors (e.g. Eigen::VectorXd)
  • Built-in scalars (e.g. double)
• NativeLieGroup: type that implements the Lie group operations as class methods. Examples:
  • smooth::SO3<float>
  • smooth::C1<double>
  • smooth::Bundle<NativeLieGroup | Eigen::Matrix<Scalar, N, 1> ...>

Both Manifold and LieGroup are defined via external type traits (traits::man and traits::lie) that can be specialized in order to define Manifold or LieGroup interfaces for third-party types.

Algorithms

Tangent space differentiation

Available for Manifold types, see diff.hpp.

Supported techniques (see smooth::diff::Type):

• Numerical derivatives (default)
• Automatic differentiation using autodiff (must #include <smooth/compat/autodiff.hpp>)
• Automatic differentiation using Ceres 2.x (must #include <smooth/compat/ceres.hpp>)

Example: calculate for i=1, 2

#include <smooth/diff.hpp>
#include <smooth/so3.hpp>
 
auto f = []<typename T>(const smooth::SO3<T> & v1, const smooth::SO3<T> & v2) {
  return (v1 * v2).log();
};
 
smooth::SO3d g1 = smooth::SO3d::Random();
smooth::SO3d g2 = smooth::SO3d::Random();
 
// differentiate f at (g1, g2) w.r.t. first argument
auto [fval1, J1] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2), std::index_sequence<0>{});
 
// differentiate f at (g1, g2) w.r.t. second argument
auto [fval2, J2] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2), std::index_sequence<1>{});
 
// differentiate f at (g1, g2) w.r.t. both arguments
auto [fval, J] = smooth::diff::dr<1>(f, smooth::wrt(g1, g2));
 
// Now J == [J1, J2]

Non-linear least squares optimization

Available for Manifold types, see optim.hpp.

The minimize() function implements a Levenberg-Marquardt trust-region procedure to find a local minimum. All derivatives and computations are done in the tangent space as opposed to e.g. Ceres which uses derivatives w.r.t. the parameterization.

A sparse solver is implemented, but it is currently only available when analytical derivatives are provided.

Example: Calculate

#include <smooth/optim.hpp>
#include <smooth/so3.hpp>
 
smooth::SO3d g1       = smooth::SO3d::Random();
const smooth::SO3d g2 = smooth::SO3d::Random();
 
// function defining residual
auto f = [&g2]<typename T>(const smooth::SO3<T> & v1) {
  return (v1 * g2.template cast<T>()).log();
};
 
// minimize || f ||^2 w.r.t. g1 (g1 is modified in-place)
smooth::minimize(f, smooth::wrt(g1));
 
// Now g1 == g2.inverse()

Piecewise polynomial curve evaluation and fitting

Available for LieGroup types, see spline/spline.hpp.

These splines are piecewise defined via Bernstein polynomials and pass through the control points. See examples/spline_fit.cpp for usage.

B-spline evaluation and fitting

Available for LieGroup types, see spline/bspline.hpp.

The B-spline basis functions have local support, A B-spline generally does not pass through its control points. See examples/spline_fit.cpp and examples/bspline.cpp for usage.

Compatibility

Utility headers for interfacing with adjacent software are included.

• compat/autodiff.hpp: Use the autodiff library as a back-end for automatic differentiation
• compat/ceres.hpp: Local parameterization for Ceres on-manifold optimization, and use the Ceres automatic differentiation as a back-end
• compat/odeint.hpp: Numerical integration using boost::odeint
• compat/ros.hpp: Memory mapping of ROS/ROS2 message types

Related Projects

• smooth_feedback utilizes smooth for control and estimation on Lie groups.

Two projects that have served as inspiration for smooth are manif—which also has an accompanying paper that is a great practical introduction to Lie theory—and Sophus. Certain design decisions are different in smooth: derivatives are with respect to tangent elements as in manif, but the tangent types are Eigen vectors like in Sophus. This library also includes the Bundle type which facilitates control and estimation tasks, as well as utilities such as differentiation, optimization, and splines. Finally smooth is written in C++20 and leverages modern features such as concepts and ranges.