mesh_function.hpp File Reference

Evaluate transform-like functions and derivatives on collocation points. More...

#include <Eigen/Dense>
#include <Eigen/Sparse>
#include <smooth/diff.hpp>
#include "mesh.hpp"
#include "smooth/feedback/utils/sparse.hpp"

Include dependency graph for mesh_function.hpp:

This graph shows which files directly or indirectly include this file:

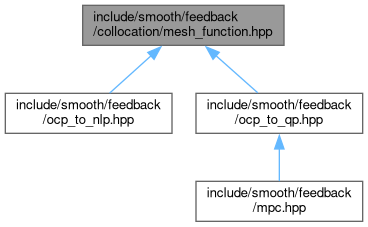
Go to the source code of this file.

Classes
struct	smooth::feedback::MeshValue< 0 >
	Result of Mesh function. More...
struct	smooth::feedback::MeshValue< 1 >
	Result and first derivative of Mesh function. More...
struct	smooth::feedback::MeshValue< 2 >
	Result, first, and second derivatives w.r.t. collocation variables. More...

Functions
template<uint8_t Deriv>
void	smooth::feedback::set_zero (MeshValue< Deriv > &mv)
	Reset MeshValue to zeros. More...
template<uint8_t Deriv, diff::Type DT = diff::Type::Default> requires (Deriv <= 2)
void	smooth::feedback::mesh_eval (MeshValue< Deriv > &out, const MeshType auto &m, auto &f, const double t0, const double tf, std::ranges::range auto &&xs, std::ranges::range auto &&us, bool scale=false)
	Evaluate function over a mesh. More...
template<uint8_t Deriv, diff::Type DT = diff::Type::Default> requires (Deriv <= 2)
void	smooth::feedback::mesh_integrate (MeshValue< Deriv > &out, const MeshType auto &m, auto &f, const double t0, const double tf, std::ranges::range auto &&xs, std::ranges::range auto &&us)
	Evaluate integral over a mesh. More...
template<uint8_t Deriv, diff::Type DT = diff::Type::Default> requires (Deriv <= 2)
void	smooth::feedback::mesh_dyn (MeshValue< Deriv > &out, const MeshType auto &m, auto &f, const double t0, const double tf, std::ranges::range auto &&xs, std::ranges::range auto &&us)
	Evaluate dynamic constraints over a mesh (differentiation version). More...

Detailed Description

Evaluate transform-like functions and derivatives on collocation points.

Definition in file mesh_function.hpp.

Function Documentation

mesh_dyn()

template<uint8_t Deriv, diff::Type DT = diff::Type::Default>
requires (Deriv <= 2)

void smooth::feedback::mesh_dyn	(	MeshValue< Deriv > &	out,
		const MeshType auto &	m,
		auto &	f,
		const double	t0,
		const double	tf,
		std::ranges::range auto &&	xs,
		std::ranges::range auto &&	us
	)

Evaluate dynamic constraints over a mesh (differentiation version).

Template Parameters

Deriv	differentiation order (0, 1, or 2)
DT	inner differentiation method (used to differentiate f)

For interval \(j\) with nodes \(\tau_i\) and weights \(w_i\) the corresponding dynamic constraints are a block of the form

\[ \begin{bmatrix} w_0 \left( f\left(t_0 + (t_f - t_0) \tau_0, x_0, u_0\right) - \sum_{k=0}^{N_j} D_{k, 0} x_k \right) \\ \vdots \\ w_{N_j-1} \left( f\left(t_0 + (t_f - t_0) \tau_{N_j-1}, x_{N_j - 1}, u_{N_j - 1}\right) - \sum_{k=0}^{N_j} D_{k, N_j-1} x_k \right) \end{bmatrix}, \]

where \(D\) is the interval differentiation matrix (see interval_diffmat() in Mesh).

This function returnes all such blocks stacked into a 1D vector.

If DT > 0 derivatives w.r.t. t0, tf, {xi} and {ui} are returned.

Parameters

out	result structure
m	mesh
f	right-hand side of dynamics
t0	initial time parameter
tf	final time parameter
xs	state parameters {xi}
us	input parameters {ui}

Definition at line 452 of file mesh_function.hpp.

mesh_eval()

template<uint8_t Deriv, diff::Type DT = diff::Type::Default>
requires (Deriv <= 2)

void smooth::feedback::mesh_eval	(	MeshValue< Deriv > &	out,
		const MeshType auto &	m,
		auto &	f,
		const double	t0,
		const double	tf,
		std::ranges::range auto &&	xs,
		std::ranges::range auto &&	us,
		bool	scale = false
	)

Evaluate function over a mesh.

Template Parameters

Deriv	differentiation order (0, 1, or 2)
DT	inner differentiation method (used to differentiate f)

Computes the expression

\[ \begin{bmatrix} f(t_0 + (t_f - t_0) \tau_0, x_0, u_0) \\ f(t_0 + (t_f - t_0) \tau_1, x_1, u_1) \\ \vdots \\ f(t_{N-1} + (t_f - t_0) \tau_{N-1}, x_{N-1}, u_{N-1}) \end{bmatrix}. \]

If DT > 0 derivatives w.r.t. t0, tf, {xi} and {ui} are returned.

Parameters

out	result structure
m	mesh
f	integrand
t0	initial time parameter
tf	final time parameter
xs	state parameters {xi}
us	input parameters {ui}
scale	scale values with quadrature weights

Definition at line 116 of file mesh_function.hpp.

mesh_integrate()

template<uint8_t Deriv, diff::Type DT = diff::Type::Default>
requires (Deriv <= 2)

void smooth::feedback::mesh_integrate	(	MeshValue< Deriv > &	out,
		const MeshType auto &	m,
		auto &	f,
		const double	t0,
		const double	tf,
		std::ranges::range auto &&	xs,
		std::ranges::range auto &&	us
	)

Evaluate integral over a mesh.

Template Parameters

Deriv	differentiation order (0, 1, or 2)
DT	inner differentiation method (used to differentiate f)

This function approximates the integral

\[ \int_{t_0}^{t_f} f(s, x(s), u(s)) \mathrm{d} s. \]

by computing the quadrature

\[ (t_f - t_0) \sum_{i = 0}^N w_i f(t_0 + (t_f - t_0) \tau_i, x_i, u_i). \]

If DT > 0 derivatives w.r.t. t0, tf, {xi} and {ui} are returned.

Parameters

out	result structure
m	mesh
f	integrand
t0	initial time parameter
tf	final time parameter
xs	state parameters {xi}
us	input parameters {ui}

Definition at line 275 of file mesh_function.hpp.

set_zero()

template<uint8_t Deriv>

void smooth::feedback::set_zero

(

MeshValue< Deriv > &

mv

)

Reset MeshValue to zeros.

If sparse matrices are compressed the coefficients are set to zero, otherwise coefficients are removed but memory is kept.

Definition at line 80 of file mesh_function.hpp.